Higher order equations, or series of ODEs are more easily solved using the Semi-Implicit Method if represented as a matrix form. Thus,
Letters in bold in the above formulation are matrix representations, and I is the identity matrix. Having represented A as a matrix, the Backward Euler can now be formulated as:
The matrix formulation of the Backward Euler negates an iterative process, but introduces a matrix inversion. One matrix inversion suffices for the set of ODE’s at each time step, since the partial derivatives are constant. For a set of n ODE’s, the matrix A is of size nXn, and the variable matrix yn is nX1. A matrix multiplication thus needs to be performed to determine y(n+1).
Press et al (Press, Teukolsky, Vetterling & Flannery, Numerical Recipes, The Art of Scientific Computing) recommend LU-decompositions for the matrix inversion process, followed by the LU-back substitution. Subroutines LUDCMP and LUBKSB can be implemented for this process.
The algorithm for the semi-implicit process can be summarized as:
1) % Define step size (h), initial function y(0), initial time t0, final time tf, eps
2) nosteps = (tf – t0)/h
3) for i ← 1 to nosteps
– Calculate matrix A
– Invoke subroutine LUCDMP for A
– B ← LUDCMP (A)
– Invoke LUBKSB to compute h*B*f(yn)
– f(yn) ← LUBKSB(h*B*f(yn))
– y[i] ← y[i-1] + f(yn)
– t0 ← t0 + h
4) % Display results
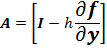

[…] matrix representation for the Backward Euler solution introduced a partial derivative term in the integration algorithm. […]
[…] matrix A is the same as the one defined earlier. The step-by-step process (which is similar to the generalized RK methods) can be summarized […]