The two-body orbit problem
Orbit equations refer to a class of ODE’s in Astronomy that describes the motion of planets due to the gravitational forces that each body exerts on the others. The two-body orbit equations are represented by the following differential equations (ref: Enright & Pryce, Two Fortran Packages for Assessing Initial Value problems, ACM Transactions on Mathematical Software, Vol. 3, No. 1, pp 1-27, 1987):
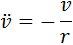
The initial values are defined by
The variable step Verner’s method was employed to solve the two-body problem using an epsilon of 0.3 for the initial values. The solutions of velocity versus displacement for u and v are shown below:
The simple pendulum and its solution
The motion of an object suspended from a string that allows free swinging can be modeled using Newton’s law. The equation for a simple pendulum, which approximates the motion to a single plane, can be written as follows:
In the above equation, g is gravity, 32.2 ft/s. Given an initial angular displacement and zero initial velocity, the above equations can be solved to obtain the angular displacement and velocity of the pendulum. The 2nd order DE has to be split up into two first order ones in order to obtain a solution.
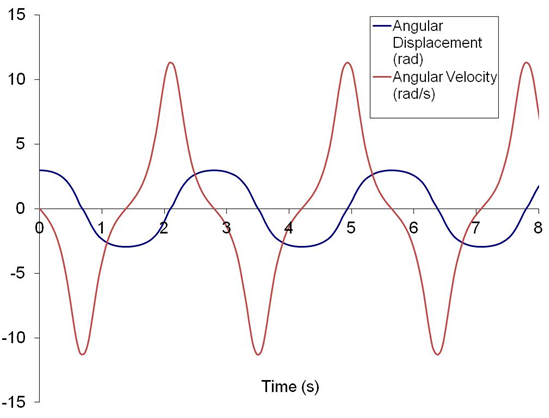
The variable-step method of Dormand & Prince was applied to solve the above IVP. The results for a 170 deg initial displacement are shown below.
A comparison of the velocity vs displacement for 45 deg and 170 deg initial values is shown below.
Variable step Fehlberg’s Method –example
Problem B2 from W.H. Enright & J.D. Pryce (Two Fortran Packages For Assessing Initial Value Methods, ACM Trans. On Mathematical Software, Vol. 13, No. 1, 1987, pp 1-27) was solved using the Variable-Step Fehlberg’s method. The equations are:
The initial conditions are 1 for all equations, with α= 3. A TOL of 1E-4 was used for the calculations, with Maxbound of 1.1 and Minbound of 0.9. The results are shown below:
The method of Verner
An example of a 7-stage method with an 8-stage error estimation was developed by Verner (Explicit Runge-Kutta Methods with Estimates of the Local Truncation Error, SIAM Journal on Numerical Analysis, Vol. 15, No. 4 (Aug., 1978), pp. 772-79). The Butcher tableau is shown below.
Once again, the generalized RK methodology can be used quite easily with the above table for the Verner’s method. The error estimate is obtained using the ycap coefficients from the last row of coefficients, and can be used to develop a variable step algorithm.
The method of Dormand & Prince
Higher order RK methods that involve 6 and higher stages of calculations at each time step are the next logical procedures. One of these methods with a 6-stage calculation, followed by a 7-stage error estimation, was developed by Dormand & Prince (Dormand & Prince, A family of embedded Runge-Kutta formulae, Journal of Computational & Applied Mathematics, Vol. 6, #1, pp 19-26). The Butcher tableau for the Dormand & Prince method is shown below.
A Handful Of Numerical Integration Techniques 
Recent Comments