Pitfalls with the variable step Euler method
While the variable step size algorithm has its advantages (of potentially reducing the number of steps required to perform the integration based on the tolerance, compared to a fixed step algorithm), one needs to be extremely vigilant of overshoots in steps.
Consider the figure from the variable step-size Euler’s approach. The inconsistencies in the plot at the circled locations are due to this phenomenon of overshoot in the step-size. The figure below shows the step-size versus time for the same problem. The overshoots in step-sizes occur at the exact instances where the “discontinuities” show up in the solution of y(x).
To avoid such discontinuities, P. Kaps & P. Rentrop (Generalized Runge Kutta Methods of Order Four with Stepsize Control for Stiff ODE’s, Numerical Mathematics, Vol. 33, Issue 1, pp 55-68, 1979) suggest bounding the steps using the following approach:
If hnew > A * hold, then hnew = A * hold
If hnew < B * hold, then hnew = B * hold
where A and B are positive constants, A > 1 and B < 1. Kaps & Rentrop quite simply suggest that A and B are chosen based on experience! Intuitively, the aim is to ensure that the step-sizes do not get too large. Conservative values for A and B can be 1.2 and 0.8, thus bounding the new step sizes to between 0.8 and 1.2 times the old step size.
The figure below shows the solution with such a bounded step size implementation, using constants A=1.1 and B=0.9.
How does one go about choosing A & B for all cases? Perhaps there are better estimates for determining step sizes out there that can simplify the process? Or perhaps it is time to advance to higher order methods in numerical integration?!
Adaptive step-size for Euler’s method
The error in the numerical estimate of the Euler’s method can be determined by performing a 1-step and 2-step integration at each time step. The absolute difference between the full-step and the two-half-step values at each time step then becomes the error estimate. Using this error estimate, iterations can be performed until the error is less than a user specified tolerance (TOL).
Two approaches can be used for this iterative process. With a fixed step approach, the future step size for every iteration can be halved from the previous step until convergence. Alternatively, the step size can be adaptively determined using the idea that the error is proportional to the square of the step size (ref. C.W. Gear, Numerical Initial Value Problems in ODE’s, and Prof. Feldman’s notes at http://www.math.ubc.ca/~feldman/math/vble.pdf).
If the error is greater than TOL, then the new step size for the iteration is
C is the constant of integration. SF is a safety factor (typically 0.9) that is used to ensure the new step does not overshoot the estimate.
The algorithm for adaptive step size Euler’s method can be thusly stated:
1) % Define original step size (h), y_half and y_full, TOL – these are defined as part of the original Euler’s loop.
2) Error = abs(y_half – y_full)
3) Do Until Error <= TOL
– Calculate hnew
– Recalculate y_half and y_full with hnew
4) Proceed to next time step
The example from Prof. Feldman’s notes was used to illustrate the concept. The IVP is:
A TOL of 0.005 was used for the analysis. The solution is shown in the figure below. Although the solutions for both the full and the half steps are practically the same with a 0.005 TOL, an interesting phenomenon can be observed at the circled locations in the figure. Is the “kink” real, or an artifact of the integration process?!
2-step Euler’s method
One technique to improve the stability of the Euler’s method is to use a 2-step approach at each step of integration. That is, given a step size h, one can perform two sub-steps, t(n) to t(n+h/2) followed by t(n+h/2) to t(n+h). Mathematically, this becomes:
The algorithm then becomes:
1) % Define step size (h), initial function y(0), initial time t0, final time tf
2) nosteps = (tf – t0)/h
3) for i ← 1 to nosteps
– Calculate derivative function f[t0,y[i-1]], and
– y[i*] ← y[i-1] + 0.5*h* f[t0,y[i-1]]
– t0 ← t0 + h/2
– Calculate f[t0, y[i*]]
– y[i] ← y[i*] + 0.5*h* f[t0, y[i*]]
– t0 ← t0 + h
4) % Display results
The example from Hairer & Lubich’s report (Numerical solution of ODE’s, source unknown) is a great example to illustrate this concept. The figure below shows the solution of the equation using a 1-step Euler method (with a step size of 0.038), and compares it with a 2-step solution. The 2-step solution has a more “smooth” behavior and hence a more stable. This is evident from the fact that the 2-step approach uses half the step size at each time step for the integration.
The 2-step Euler serves other practical uses too. Such an approach can be used to estimate the error in the solution (which can prove to be useful if an analytical solution is unknown). Based on this error at a particular step, the 2-step approach can potentially be used to modify the step size for future steps. This would pave way for an adaptive step size approach (contrast this with the existing approach which uses a fixed step size for all time steps).
The Trapezoidal Method
The Trapezoidal method of numerical integration is based on the premise that integration (which is the area under a curve) between two points on the abscissa can be approximated by a straight line between the corresponding ordinates. Mathematically, this can be represented as follows:
The similarity to the Backward Euler’s method is evident. The solution of the Trapezoidal method requires an iterative procedure at each time step to arrive at a solution for yn. A root-finding algorithm once again comes in handy for this iterative process.
A simplified algorithm for the Trapezoidal method can be:
1) % Define step size (h), initial function y(0), initial time t0, final time tf, eps
2) nosteps = (tf – t0)/h
3) for i ← 1 to nosteps
– Calculate derivative function f[t0,y[i]]
– Iterate until y[i] – (y[i-1] + 0.5*h*{ f[x(i-1), y(i-1)] + f[x(i), y(i)]}) < eps
– t0 ← t0 + h
4) % Display results
Eq. 203(a) from J.C.Butcher, Numerical Solution of ODE’s, 2nd Edition, was solved using the Trapezoidal method. The equations for the IVP are:
With y1(0)=1 and y2(0)= 0. A step size of 0.005, and eps of 1E-8 were used for the solver. The plots for y1 and y2 are shown below.
Backward Euler – part 2
The figure below shows the solution to the ODE from Curtiss & Hirschfelder, previously presented here. The figure below, however, was solved using the Backward Euler’s method. The Backward Euler clearly has better convergence and stability compared to the Forward Euler. Irrespective of the step size ‘h’, the solutions clearly converge. The increase in calculation time from the iteration at each time step is made up for by the superior stability characteristics of this method.
So, which of the above solutions is now the “correct” one?!
The backward Euler’s method
The examples in the previous post suggested the importance of step-size ‘h’ for numerical integration, and how improper choices of ‘h’ may lead to a divergent solution. The Euler’s method presented in the former post, as indicated earlier, marched from time tn to tn+1 using the knowledge of the solution at time tn. This method is also known as the Forward Euler, since it marches forward in time.
The forward Euler at time tn uses the derivative at tn to march to tn+1. Instead, if the derivative is obtained at time tn+1, the method becomes the Backward Euler. Mathematically, it is represented by the following equation:
Since the function y(x) appears on both sides of the equation, one can no longer simply march forward between time steps. Rather, one needs to perform an iterative root-finding algorithm to determine y(x) at each time step
A simplified algorithm for the Backward-Euler can be summarized as follows:
1) % Define step size (h), initial function y(0), initial time t0, final time tf, eps
2) nosteps = (tf – t0)/h
3) for i ← 1 to nosteps
– Calculate derivative function f[t0,y[i]]
– Iterate until y[i] – (y[i-1] + h*f[x(i), y(i)]) < eps
– t0 ← t0 + h
4) % Display results
‘eps’ is a user-specified tolerance value for the root-solver. The solver iterates until the equation at each time step is less than ‘eps’. The value that satisfies this condition is the numerical solution at that time. The iteration can be performed using any root-finding algorithm like the Bisection or the Newton-Raphson method. A modified form of the subroutine ‘rtbis’ adapted from Numerical Recipes, (The art of scientific computing, Press et al, 2nd ed.) was used for this exercise.
The Backward Euler’s method was applied to the following problem (Atkinson et al, Numerical Solution of Ordinary Differential Equations, Eg. 5.8).
The solution is shown in fig. 1.


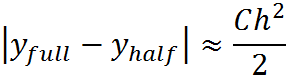



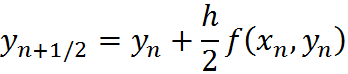


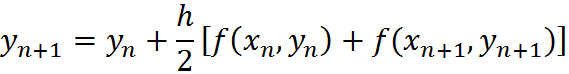




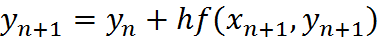


Recent Comments